How All-Reduce Affects the Backward Pass

27 May, 2025

Last updated 2 months, 4 weeks

In distributed training there are often operations where some unsharded tensor $x$ is acted on by a sharded network to produce a sharded output $y_r$, where $r$ is the number of ranks across which the operation is sharded. This operation can be thought of as $y_r=F(x,...)$ where $F$ may also take other tensors as input- sharded or not, represented by “$...$”

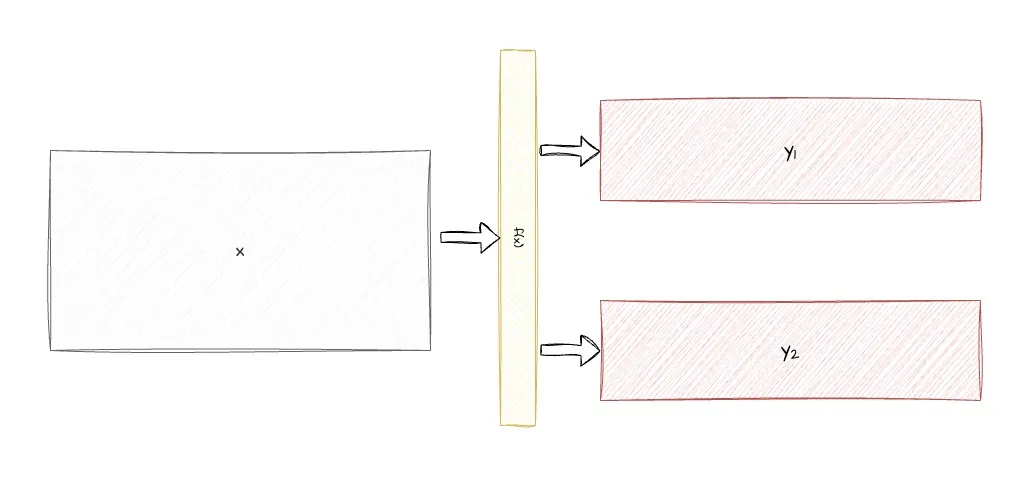
Here $F$ will be a layer in a model, $y_r$ will be the sharded output of a model while $x$ is the input tensor. The input tensor either be from the residual stream which, still needs to flow gradients backwards for optimising prior layers- or it may be the initial embeddings after tokenisation- which would still need to flow gradients backwards to optimise the embeddings.

Hence, when calculating the backward pass, we will need to consider $\frac{\partial L}{\partial x}$, which by the chain rule will be equal to

Since each GPU in a distributed training will only have one shard $y_r$ available to it (the $r=\text{rank}$ of the GPU), so a sum of all calculated outputs in the GPU is required in order for each rank to calculate the full gradient of $\frac{\partial L}{\partial x}$. This is why training setups like in MegatronLM require an all reduce in the backward pass prior to optimisation as otherwise the gradients on each rank would diverge.

In practise, since we do the inverse of the operation of an All-Reduce in the backward pass, when we have a sharded input to an unsharded output, our backward pass for the All-Reduce is just the identity operator, since the sharded input $x_r$ will have a gradient of

where there’s no sum required since the output is already whole.

This means the following:

• Forward pass of sharded input to unsharded output ($x_r$ → $y$): backward pass will be the identity operator $I$ and not require any all reduces
• Forward pass of unsharded input to sharded output ($x$ → $y_r$): backward pass will be the All-Reduce operation

#AI #Math